关于函数的复合运算

关于函数的复合运算

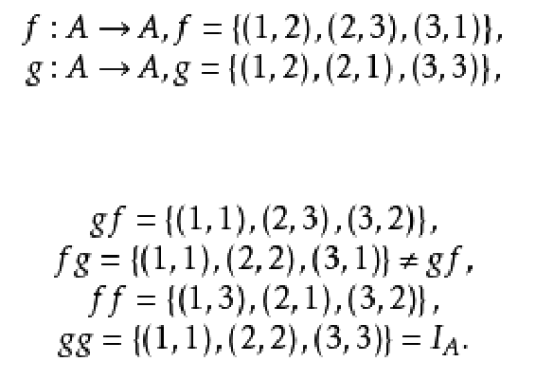
关于函数的复合运算复合函数，是按一定次序把有限个函数合成得到的函数，对两个函数f：A关于函数的复合运算→B，g：B→C，由h(x)=g(f(x))(x∈A)确定的函数h称为f与g的复合函数，记为g°f，这样，g°f是A到C的函数，(g°f)(x)=g(f(x))，它的值域是g(f(A))，记号“°”表示两个函数的复合，它是二元运算.这个运算不满足交换律，即一般来说g°f≠f°g，但它满足结合律：对f：A→B，g：B→C，h：C→D，有h°(g°f)=(h°g)°f，于是可以定义h°g°f=h°(g°f)=(h°g)°f，一般地，对n+1个满足Bi⊆Ai+1(i=1，2，…，n)的函数fi：Ai→Bi(i=1，2，…，n+1)可以定义n重复合函数fn+1°fn°…°f1，任给两个函数f：A→B，g：C→D，当且仅当f(A)⊆C时可以得到复合函数g°f：A→D；当且仅当g(C)⊆A时可以得到f°g：C→B，当函数用变量表示为t=f(x)，y=g(t)，且f的值域含于g的定义域时，称t为复合函数y=g(f(x))的中间变量，函数的复合是研究函数的一种工具，一方面它提供了构造各式各样的新函数的方法；另一方面，为研究复杂的函数，常将它们看成一些简单函数的复合(求函数的导数时常这样做) 。

想要了解更多“关于函数的复合运算”的信息，请点击：关于函数的复合运算百科